Wie wichtig ist es, Parteitage und Stammtische in die Mitte der Region zu legen?
Abstract
Der Unterschied zwischen optimaler und suboptimaler Lage eines Treffpunktes über die Fläche verteilter Teilnehmerinnen erweist sich als kleiner als vermutet. Das legt nahe, andere Kriterien (Lage an Verkehrslinien, preisgünstige Veranstaltungsräume und Übernachtungsmöglichkeiten, besonders kurze Anreise für Transporteure voluminöser Gerätschaften usw.) in Betracht zu ziehen.Einleitung
Piratenintern hatten wir kürzlich (Mittelerde-Barcamp) die Diskussion, wo zentrale Veranstaltungen (von Stammtisch bis hin zum BPT) stattfinden sollten. Da ist es naheliegend, den Mittelpunkt des Einzugsgebietes zu nehmen (über eine Gewichtung nach Teilnehmerinnendichte usw. kann man natürlich nachdenken, das ändert das Problem aber nur marginal). Für mich ergab sich daraus zwangsläufig die Frage: Wie optimal ist das wirklich, und wie groß ist der Vorteil?Ergebnisse
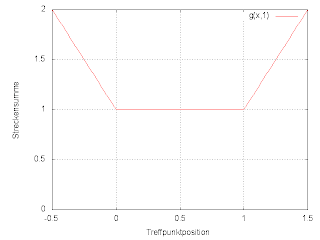
Nehmen wir zuerst den einfachsten Fall: Wir haben zwei Personen A und B, und die wohnen an den Positionen "0" und "1" einer geraden Strecke. Dann sind alle Punkte im Innern der Strecke gleichwertig - wenn wir den Treffpunkt ein wenig nach rechts verschieben, muss A um diesen Betrag weiter fahren, B entsprechend weniger. Erst bei einem Treffpunkt außerhalb des Einzugsgebietes nimmt die Fahrstrecke zu.Zu dritt ändert sich das ein wenig - B wohnt jetzt in der Mitte, die Summe der Fahrstrecken für A und C ist weiterhin konstant, aber bei außermittiger Lage des Treffpunktes muss B fahren. Jetzt sind die Endpunkte etwas (um 50%) schlechter als der Mittelpunkt.
Man sieht schon, wo das hingeht - wenn wir die Anzahl hochsetzen, erhalten wir eine Parabel im Innern und eine zur Parabel tangentiale lineare Steigerung außen. Hier ist ein Beispiel für 40 Teilnehmerinnen:
Wie man sieht, ist die Streckensumme für den ungünstigsten sinnvollen Treffpunkt jetzt doppelt so groß wie für den Mittelpunkt. Zweitens bedenke man, dass Parabeln in der Nähe des Scheitelpunktes relativ flach verlaufen - wenn man mäßig vom Optimum abweicht, ist der Schaden gering (das gilt allgemein für Optimierungen stetiger Größen). So beträgt die optimale Summe (d.h. Treffpunkt bei 0.5) im letzten Beispiel 10.26 Einheiten. Wenn man um 10% der Ausdehnung des Einzugsgebietes abweicht, wächst sie nur um 0.39 Einheiten auf 10.65.
In zwei Dimensionen ist das etwas schwieriger. Wie beginnen mit der kleinsten Variante: Ein Quadrat mit vier an den Ecken wohnenden Teilnehmerinnen. Das Optimum liegt klar in der Mitte, aber ist nicht mehr komplett gleichgültig. Wenn man den Treffpunkt entlang der Diagonalen AC verschiebt, ändert sich für die Summe der Entfernungen für A und C nichts. Für B und D steigt aber der Aufwand geringfügig - die Hypothenuse eines rechtwinkligen Dreiecks ist immer länger als die längste Kathete. Allerdings ist dieser Unterschied vernachlässigbar klein, wenn die kurze Kathete sehr kurz ist. Im Extremfall (Treffpunkt an einer der Ecken) ist die Summe um ca. 20% größer als das Minimum.
Auch hier nimmt der Nachteil eines dezentralen Treffpunktes zu, wenn Leute im Innern der Fläche wohnen.
Für 9 Personen sieht das Diagramm so aus:
Der Nachteil der Ecken gegenüber dem Mittelpunkt beträgt jetzt 52% (7.36 statt 4.83 Einheiten).Jetzt nehmen wir wieder eine Teilung der Kantenlänge in 39 Teile (d.h. 40×40=1600 Teilnehmerinnen). Das Bild sieht dann so aus:
Jetzt ist die Eckposition doppelt so schlecht wie der Mittelpunkt. Aber eine Verschiebung des Treffpunkts um je eine Zehnteleinheit nach Norden und Osten bewirkt nur eine Verschlechterung um 4.4%.
Methoden
Auf Methoden der höheren Mathematik wurde in der gesamten Arbeit verzichtet, wenn auch der eindimensionale Fall im Grenzwert von ∞ vielen Teilnehmern damit triviel zu behandeln ist. Alle Berechnungen wurden unmittelbar in gnuplot durchgeführt und dargestellt. Hier sind die verwendeten Funktionsdefinitionen. User-Defined Functions:
f(x,a,n)=abs(x-(1.0*a/n))
g(x,n)=gs(x,n,n)
gs(x,m,n)=(m<0)?0:(f(x,m,n)+gs(x,m-1,n))
hyp(x,y)=sqrt(x*x+y*y)
F(x,y,a,b,n)=hyp(x-1.0*a/n,y-1.0*b/n)
G(x,y,n)=Gss(x,y,n,n)
Gss(x,y,m,n)=(m<0)?0:(Gss(x,y,m-1,n)+Gs(x,y,m,n,n))
Gs(x,y,m,r,n)=(r<0)?0:(Gs(x,y,m,r-1,n)+F(x,y,m,r,n))
Dabei sind die Funktionen für den eindimensionalen Fall mit Kleinbuchstaben, die für den zweidimensionalen Fall mit Großbuchstaben bezeichnet. f(x,a,n) liefert die Fahrstrecke für Teilnehmerin a (von 0..n) zum Treffpunkt x, analog F(x,y,a,b,n). n+1 bezeichnet jeweils die Zahl der Teilnehmerinnen entlang einer Dimension. gs, Gs und Gss sind rekursive Hilfsfunktionen (gnuplot erlaubt Rekursion, sofern man mit Hilfe des ternären Operators die Terminierung garantiert). Da die Division ganzer Zahlen in gnuplot auch als Ganzzahldivision ausgeführt wird, wurde sicherheitshalber an allen relevanten Stellen "1.0*" eingebaut (da der Funktionsparser in gnuplot von links nach rechts arbeitet, reicht das - richtig sicher wäre "(1.0*a)/n" statt "1.0*a/n").Für die Forschungen wurden keine tentakeligen Versuchstiere belästigt oder getötet (tentakellose sind irrelevant).